সরল ও স্পন্দন গতি(Simple and Harmonic Motion)

নবম-দশম শ্রেণি (দাখিল) - পদার্থ বিজ্ঞান - তরঙ্গ ও শব্দ (Waves and Sound) | | NCTB BOOK

একটা স্প্রিংয়ের নিচে একটা স্তর লাগিয়ে সেটা টেনে ছেড়ে দিলে এটা উপরে-নিচে করতে থাকে। (তৃতীয় এবং চতুর্থ অধ্যায়ে আমরা এই গতিটি ব্যাখ্যা করেছি।) আমরা দেখেছি ঘর্ষণের জন্য বা অন্যান্যভাবে শক্তি ক্ষয় হয় বলে এটা একসময় থেমে যায়। তা না হলে এটা অনন্তকাল উপর-নিচ করতে থাকত। আমরা এটাও দেখেছি সরল স্পন্দন গতিতে স্প্রিংয়ের সাথে লাগানো ভরটির শক্তি গতিশক্তি এবং বিভব শক্তির মাঝে বিনিময় করে এবং এসব ঘটে কারণ স্প্রিংয়ের বলটি হুক এর সূত্র মেনে চলে। হুকের সূত্রটি আবার মনে করিয়ে দেওয়া যায়, স্প্রিংয়ের ধ্রুব যদি হয় k, ভর যদি হয় m এবং অবস্থান যদি হয় x: তাহলে তার ওপর আরোপিত বল F হচ্ছে

F = -kx

হুকের সূত্রের কারণে যে ছন্দিত বা স্পন্দন গতি হয় সেটাকে বলে সরল স্পন্দন গতি। পদার্থবিজ্ঞানের সবচেয়ে গুরুত্বপূর্ণ গতিগুলোর একটি হচ্ছে এই গতি।

তোমাদের এই বইয়ে এটা বের করে দেখানোর সুযোগ নেই কিন্তু জানিয়ে রাখতে ক্ষতি কী? যদি একটা স্প্রিংয়ের খুব হয় k এবং ভর হয় m তাহলে ভরটির দোলনকাল হবে

$T = 2 π \sqrt{\frac{m}{k}}$

যদি এটা স্প্রিং না হয়ে একটা সুতার ঝোলানো পেন্ডুলাম হতো এবং সুতার দৈর্ঘ্য হতো।আর মাধ্যাকর্ষণজনিত ত্বরণ হতো তাহলে দোলনকাল হতো:

$T = 2 π \sqrt{\frac{l}{g}}$

(না, কোনো ভুল হয়নি, তুমি একটা হালকা ভরই ঝোলাও আর ভারী ভরই ঝোলাও দোলনকাল একই থাকবে, এটা ভরের ওপর নির্ভর করে না।)

একটা স্প্রিংয়ের নিচে একটা ভর লাগিয়ে রেখে দিলে ভরটা স্প্রিংটাকে টেনে একটু লম্বা করে সেই অবস্থানে স্থির হয়ে থাকে। স্প্রিংয়ের এই দৈর্ঘ্যটাকে বলা যায় সাম্য অবস্থা (চিত্র 7.010) |
এখন যদি ভরটাকে টেনে একটু নিচে a দূরত্ব নামিয়ে এনে ছেড়ে দিই (চিত্র 7.01-1) তাহলে ভরটা উপরের দিকে উঠতে থাকবে, সাম্য অবস্থা পার হয়ে এটা উপরে ৫ দূরত্বে উঠে যাবে, তারপর আবার নিচে নামতে থাকবে, সাম্য অবস্থা পার হয়ে নিচে নেমে যাবে এবং এটা চলতেই থাকবে।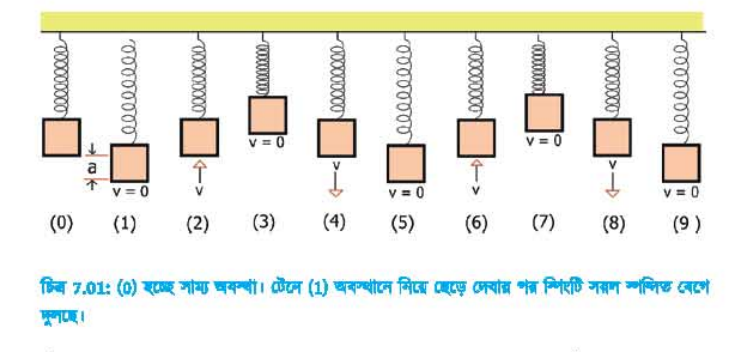

ভরটা যখন 2 $\to$ 3 $\to$ 4 $\to$ 5 অবস্থান শেষ করে যে অবস্থানে শুরু করেছিল ঠিক একই অবস্থানে (6) একইভাবে ফিরে আসে (উপরের দিকে v বেগে গতিশীল) তখন আমরা বলি একটা পূর্ণ স্পন্দন হয়েছে। মনে রাখতে হবে 2 $\to$ 3 শেষ করে 4 এলেও কিন্তু যে অবস্থান থেকে শুরু করেছে সেই অবস্থানে ফিরে আসবে কিন্তু এটা পূর্ণ স্পন্দন নয় কারণ প্রথম 2 অবস্থানটিতে উপরের দিকে যাচ্ছে এবং পরের 4 অবস্থানটিতে নিচের দিকে যাচ্ছে, কাজেই এক অবস্থানে একইভাবে ফিরে আসা হলো না।

সরল স্পন্দন গতি বিশ্লেষণ করতে হলে আমাদের কয়েকটা রাশি ব্যাখ্যা করে নেওয়া ভালো। প্রথমটি হতে পারে পর্যায় কাল (Time Period) বা দোলনকাল T। একটা পূর্ণ স্পন্দন হতে যে সময় নেয় সেটা হচ্ছে পর্যায়কাল বা দোলনকাল। কম্পাঙ্ক f হচ্ছে প্রতি সেকেন্ড পূর্ণ স্পন্দনের সংখ্যা অর্থাৎ $f = \frac{1}{T}$ পর্যায়কাল T যদি সেকেন্ডে প্রকাশ করি তাহলে f এর একক হচ্ছে হার্টজ (Hz)।

সরল স্পন্দিত গতিতে বিস্তার হচ্ছে সাম্যাবস্থা থেকে সবচেয়ে বেশি উপরে ওঠা (কিংবা নিচে নামা ) দূরত্ব। 7.01 চিত্রে যেভাবে দেখানো হয়েছে সেখানে বিস্তার হচ্ছে a.

এর পরের রাশিটি হচ্ছে দশা (Phase), স্প্রিংয়ে লাগানো ভরটি যখন ওঠানামা করছে, তখন কোনো এক মুহূর্তে যদি ভরটির দিকে তাকাই তাহলে আমরা দেখব সেটি সাম্যাবস্থা থেকে কোনো একটি দূরত্বে থাকবে, সেই অবস্থানটি হচ্ছে তার দশা। সরল স্পন্দন গতিতে ভর এবং স্প্রিংয়ের এই নির্দিষ্ট অবস্থাটি হুবহু একইভাবে ফিরে আসবে আবার ঠিক এক পর্যায়কাল পরে। পদার্থবিজ্ঞানের ভাষায় বলা যায় সরল স্পন্দন গতিতে কোনো এক মুহূর্তে যে দশা হয় এক দোলনকাল পর আবার সেই দশা ফিরে আসে।

Content added By